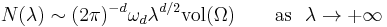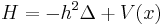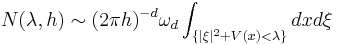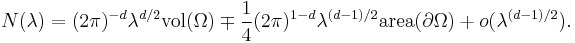Weyl law

In 1911 Hermann Weyl proved that for positive Dirichlet Laplacian number of eigenvalues (counting their multiplicities) of Dirichlet Laplacian (i.e. Laplacian 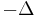$-\Delta$ with Dirichlet boundary condition 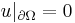$u|_{\partial\Omega}=0$ ) in the bounded domain 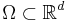$\Omega\subset \mathbb{R}^d$ not exceeding $\lambda$ has asymptotics

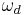$N(\lambda)\sim (2\pi)^{-d} \omega_d \lambda ^{d/2}\mathrm{vol} (\Omega)\qquad \text{as}\ \ \lambda\to %2B\infty$

where $\omega_d$ is a volume of the unit ball in 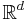$\mathbb{R}^d$ ^[1]. In 1912 he provided a new proof based on variational methods^[2].

1 Improved remainder estimate
2 Generalizations
3 Counter-examples
4 Weyl conjecture
5 References

Improved remainder estimate

Remainder estimate above 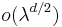$o(\lambda^{d/2})$ has been improved by many authors up to 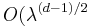$O(\lambda^{(d-1)/2}$ ) and even to two-term asymptotics with the remainder estimate 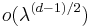$o(\lambda^{(d-1)/2})$ (Weyl conjecture) or even marginally better.

Generalizations

Weyl law has been extended to more general domains and operators, for Schrödingier operator

$H=-h^2 \Delta %2B V(x)$

it was extended to

$N(\lambda,h)\sim (2\pi h)^{-d} \omega_d \int _{\{ |\xi|^2 %2B V(x)<\lambda \}} dx d\xi$

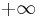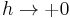as $\lambda$ tending to $%2B\infty$ or to a bottom of essential spectrum and/or $h\to %2B0$ .

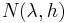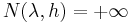Here $N(\lambda,h)$ is the number of eigenvalues of $H$ below $\lambda$ unless there is essential spectrum below $\lambda$ in which case $N(\lambda,h)=%2B\infty$ .

In the development of spectral asymptotics the crucial role was played by variational methods and microlocal analysis.

Counter-examples

However extended Weyl law fails in certain situations. In particular extended Weyl law "claims" that there is no essential spectrum if and only if the right-hand expression is finite in for all $\lambda$ .

If we consider domains with cusps (i.e. "shrinking exits to infinity") then the (extended) Weyl law claims that there is no essential spectrum if and only if the volume is finite. However for Dirichlet Laplacian there is no essential spectrum even if the volume is infinite as long as cusps shrinks at infinity (so the finiteness of the volume is not necessary).

On the other hand, for Neuman Laplacian there is an essential spectrum unless cusps shrinks at infinity faster than the negative exponent (so the finiteness of the volume is not sufficient).

Weyl conjecture

Weyl conjectured that in fact

$N(\lambda)= (2\pi)^{-d}\lambda ^{d/2}\mathrm{vol} (\Omega)\mp \frac{1}{4} (2\pi)^{1-d}\lambda ^{(d-1)/2}\mathrm{area} (\partial \Omega) %2Bo (\lambda ^{(d-1)/2}).$

Remainder estimate 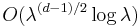$O(\lambda^{(d-1)/2}\log \lambda)$ was proven by Richard Courant (1922). For compact closed manifolds remainder estimate 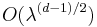$O(\lambda^{(d-1)/2})$ was proven by Boris Levitan 1952; remainder estimate 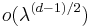$o (\lambda ^{(d-1)/2})$ was proven by Hans Duistermaat and Victor Guillemin under assumption that the set of periodic bicharacteristics has measure 0^[3].

For Euclidean domains with the boundaries remainder estimate 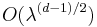$O(\lambda^{(d-1)/2})$ was proven by Robert Seeley ^[4]; remainder estimate 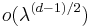$o (\lambda ^{(d-1)/2})$ was proven by Victor Ivrii under assumption that the set of periodic billiards has measure 0^[5] who also conjectured that this assumption is fulfilled for all bounded Euclidean domains with smooth boundaries.

Later similar results were obtained for wider classes of operators.

References

^ Über die asymptotische Verteilung der Eigenwerte, Nachrichten der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 110–117 (1911).
^ 'Das asymptotische Verteilungsgesetz linearen partiellen Differentialgleichungen, Math. Ann., 71:441–479 (1912).
^ The spectrum of positive elliptic operators and periodic bicharacteristics. Invent. Math. , 29(1):37–79 (1975).
^ A sharp asymptotic estimate for the eigenvalues of the Laplacian in a domain of 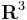$\mathbf{R}^3$ . Advances in Math.}, 102(3):244–264 (1978).
^ Second term of the spectral asymptotic expansion for the Laplace–Beltrami operator on manifold with boundary. Funct. Anal. Appl. 14(2):98–106 (1980).